Jeg elsker både vakre farger

og vakre kurver:

Noen ganger setter jeg meg ned og tegner kurver på frihånd, både blomster og hjerter, faktisk:

Andre ganger vil jeg ha hjertene mine så symmetriske at jeg bruker datamaskinen til å tegne kurvene, for eksempel i powerpoint,

eller i statistikkprogrammet R:

R-koden finner du her: https://maggielinyu.wordpress.com/2012/02/25/valentinesgift/
Jeg er oppriktig glad i hjerte og gjenkjenner dem overalt i naturen (det tror jeg ikke at jeg er alene om),

og noen ganger gjenkjenner jeg dem til og med i dataene mine (selv om det ikke er hjertesykdom jeg vanligvis forsker på):

Da er det fristende å tegne inn et hjerte, enten på frihånd, eller ved å bruke R:

Frihåndshjerte i blått, og programmert R-hjerte i rosa.
Ingen av disse hjertekurvene passet helt perfekt til de observerte datapunktene, men det er heller ikke mulig, for som alltid med observasjoner er også disse rosa prikkene i hjerteformasjon litt rufsete i kantene. Det er imidlertid mulig å tegne både frihåndshjertet og den datamaskintegnede hjertekurven slik at de passer bedre til de rufsete dataene.
Hvis vi skal få datamaskinen til å tegne det beste tilpassede hjertet automatisk, trenger vi en formel for hjertefasongen. Denne figuren viser hvordan de matematiske formlene til seks ulike hjertekurver ser ut:

For dem som lager metoder for automatisk gjenkjenning av innhold i bilder, enten det er hjerter, ansikter eller bygninger, handler jobben om å finne den versjonen av en formel som passer best til det dataene viser.
Vi som ikke jobber med dette, kan nøye oss med å kose oss med kurvene. <3 <3 <3 <3 !
For statistikerne er det ikke hjertekurver, men derimot normalfordelingskurver som får hjertet til å banke.

Mange fenomener som kan måles viser seg nemlig å ha omtrent denne fordelingen av verdier:

Det betyr at det er omtrent like mange verdier på hver side av et gjennomsnitt, og få verdier som er svært langt fra gjennomsnittet.
Blant de mange tingene vi kan måle som har omtrent denne fordelingen, finner vi for eksempel:
Fødselsvekt,
Jeg har med vilje fjernet skalaene i disse fire figurene for at vi skal se på fasongen på kurene. Her i fødselsvekteksemplet er det litt flere ekstreme verdier på venstre side av midten enn høyre side. Det er fordi vi nå heldigvis er i stand til å redde de for tidlig fødte barna med fødselsvekt helt ned i noen hundre gram. De er dermed 3 kilo lettere enn gjennomsnittet på ca 3 og en halv kilo. Men det er heldigvis ikke tilsvarende mange barn som veier tre kilo mer enn gjennomsnittet, så halen i fordelingen er kortere på høyre side av midten enn på venstre side av midten. En slik skjevhet er i strid med normalfordelingens fasong, men den kan allikevel være en ganske god modell for det vi ser.
høyde,

Her er det lite skjevhet å se, men denne fordelingen er kanskje litt for bred over skuldrene til at det egentlig er helt slik en normalfordeling skal se ut. Igjen: Allikevel passer normalfordelingsfasongen ganske godt.
målefeil,

Oioi, denne var lekker! Ingen skjevhet, ingen brede skuldre, ingen ekstremverdier, her passer normalfordelingen som hånd i hanske! Det samme gjelder for
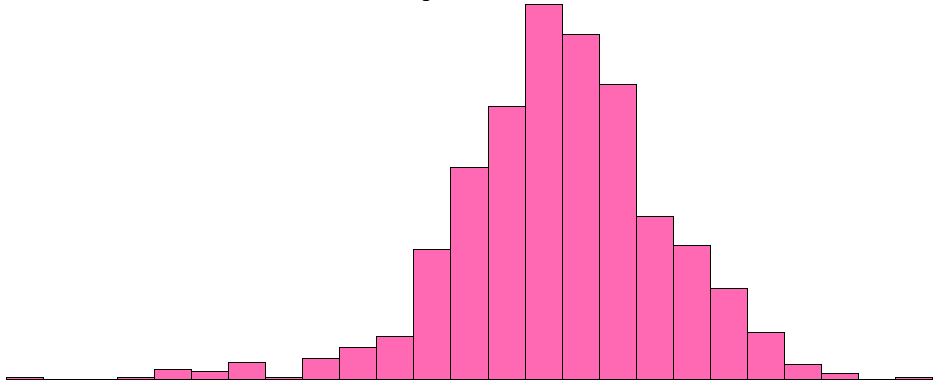
fastende blodsukker i en gruppe gravide kvinner,

og da er det fristende å tegne inn en normalfordeling, enten på frihånd, eller ved å bruke R:
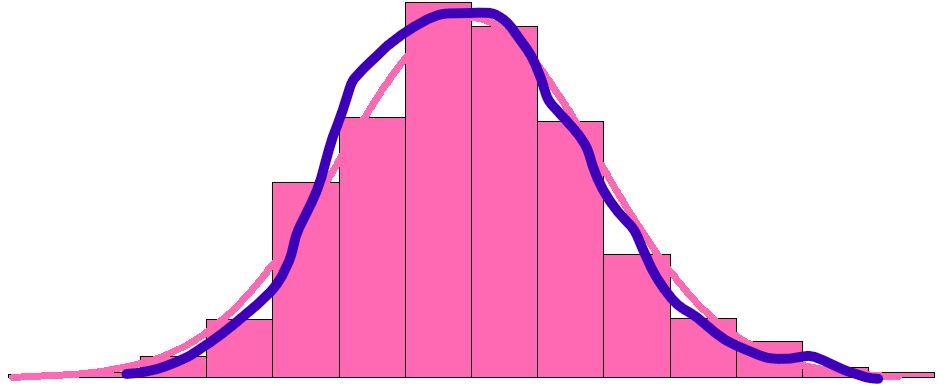
Frihåndsnormalfordeling i blått, og programmert normalfordeling (den aller beste) i rosa.
Som dere ser, er ingen av disse figurene så glatte og pene som normalfordelingen, men akkurat som hjertefasongen, gjenkjenner vi den vakre kurvefasongen allikevel: Symmetrisk, kirkeklokkeformet, og med få ekstreme verdier i begge ender.
For statistikere som jobber med analyse av data, handler noe av jobben ofte om å vurdere om normalfordelingen passer til det som må være normalfordelt for at analysene skal gi riktig resultat.
Men alle som ikke jobber med dette, kan nøye seg med å strikke de vakre kurvene*. <3 <3 <3 <3 !

En annen variant av normalfordelingsskjerfet. Andre farger, men samme kurve.
Her er første del av oppskriften i årets samstrikkeprosjekt:
Oppskrift på normalfordelingsskjerf, del 1
Du trenger:
Garn i tre farger og en middels lang rundpinne som passer garnet, men helst en størrelse større enn det som er angitt på garnet. Se gårsdagens innlegg med mer detaljer om garn og pinner. (Jeg har tjuvstartet og ser nå at med pinne 6 og refleksgarn fra Gjestal (50g=50 meter, kanskje det u-drøyeste garnet jeg noen gang har strikket med), trenger jeg 1+4+9 50-grams nøster. Hvis du vet at du strikker løst, bør du beregne et nøste ekstra i den fargen det skal være mest av, så du er sikker på at du har nok.)

Mitt fargevalg. Siden det svarte Reflex-garnet fra Järbo er litt tynnere enn Gjestal sitt, sper jeg på med en tråd svart Inca. Og jeg trenger 4 nøster mørk grå og 9 nøster lys grå. Godt jeg er en garnhamster med nok garn å ta av.
Jeg har planlagt å markere midten av skjerfet med perler, så hvis du vil gjøre det samme, trenger du etter hvert også inntil 79 perler med størrelse og farge som passer til garnet.
Normalfordelingsskjerfet strikkes på tvers i rillestrikk. En rille er to omganger rettstrikk.
Legg opp 2 m og strikk 10 riller (20 omg) med 2 m. Det blir finest hvis du strikker begge maskene, og ikke løfter av den første i omgangen.

På neste omg, øk 1 m mellom de to maskene. Det blir penest om du øker i løkka som ligger i forkant av den siste masken på pinnen.

Strikk 6 riller med 3 masker.
Resten av økningene skjer på rettsiden av strikketøyet, like før nest siste maske på omgangen. Pass på at økingene blir løse nok, hvis ikke vil kanten nederst bøye seg.
Etter de 6 rillene med 3 masker:
6 riller med 4 masker
4 riller med 5 masker
3 riller med 6 masker
4 riller med 7 masker
3 riller med 8 masker
2 riller med 9 masker
3 riller med 10 masker
Du har nå strikket 2,2% av skjerfet ditt.
Bytt farge.
Tips: Når jeg strikker normalfordelingsskjerf, skriver jeg av (deler av) tabellen på en lapp og stryker ut etter hver rille, samtidig som jeg bruker maskemarkører (jeg markerer også det på lappen), så jeg ikke går i surr. Her hadde jeg bare binders, så da ble det maskemarkøren.

Refleksgarn: Foto uten blits.

Refleksgarn: Foto med blits. Hoho!
Neste del av oppskriften kommer i morgen.

Hull i sekken, sier du? Neida, det er bare refleksgarn.
* Det finnes selvsagt en formel for normalfordelingen også, og det er den jeg har tatt utgangspunkt i når jeg har brukt statistikkprogrammet R for å lage oppskriften.


